SPECIAL NOTE RE MD-DC-VA Germantown Meeting Presentation:

I made an error in my presentation at the Germantown meeting, 11/5/05.  The envelope or boundary curve for the region swept out by sliding a ladder around a corner may not arise as the discriminant of a quadratic equation, as I claimed. My error was in confusing two different families of lines.  For the ladder problem, when I attempt to ascertain whether or not a given point lies on a line in the family of lines, I end up with a quartic equation.  It may be that a different algebraic approach might lead to a quadratic, but this seems dubious to me now.  It may also be that the discriminant of the quartic vanishes on the envelope or boundary curve, but I have not verified that.

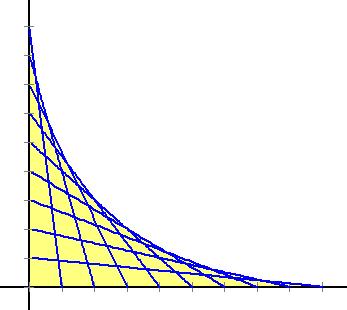
The quadratic comments are accurate in the context of a different family of lines, one for which the sum of the x and y intercepts is a fixed constant.  This is actually a common design for string art.  For example, take one line with y intercept 9 and x intercept 1,  then create a second line with y intercept 8 and x intercept 2, and continue in like fashion, repeatedly incrementing the x and y intercepts by 1 and -1, respectively.  This is shown in the figure below.
 
If we let p be the x intercept for each line, and use that as the parameter for this family of lines, then we can express the equation for such a line as follows:

(10 - p) x + py = p(10 - p)

The envelope in this case is a parabola with axis of symmetry along the line y = x, and the equation of the parabola can be obtained by using the discriminant of a quadratic equation.  

Here is how that works:  let (x , y) be a fixed but arbitrary point in the first quadrant, and ask Does this point lie on the line for some value of the parameter p?  To find out, solve the equation for p in terms of x and y.  The equation is clearly quadratic in p and can be expressed in the form

and the discriminant is given by D = (y - x - 10)² - 40x.  If D > 0 then there are two solutions, indicating that the point (x , y) is on two of the lines in the family.  In this case, the point is in the shaded part of the first quadrant.  If D < 0 there are no solutions.  This means that the point (x , y) is not on any of the lines, and so is in the part of the plane that is left unshaded.  The boundary between these two regions is the envelope of the family of lines, and this corresponds to the points (x , y) for which D vanishes.  Thus we see that the envelope curve has the equation

(y - x - 10)² = 40x

for this family of lines.