Animation for Lill's Method
by Dan Kalman

Lill's Method is a graphical representation of the roots of a polynomial, as described in my book Uncommon Excursions. It was first presented by Lill, an Austrian military engineer, in 1867, and has been described in print in English several times over the intervening years. For more on Lill's Method, see Bradford's site http://www.concentric.net/~Pvb/ALG/rightpaths.html.

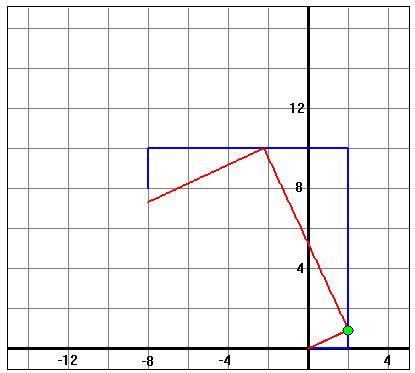Below there are links to some animated images showing Lill's Method in action.   In all the images, there are two polygonal paths, one in red and one in blue.  The legs of the blue path correspond to the coefficients of a given polynomial.  The path is drawn starting at the origin, and executing a series of right angle turns. The red path also is drawn with right angle turns. It begins at the origin as well, and starts out at a prescribed angle q. Each red leg ends on a blue leg, or on the line containing that leg. The first red leg ends on the second blue leg; the second red leg on the third blue leg; etc. This is illustrateed in the figure at left for the polynomial p(x) = 2x³+10x²+10x+2 at an angle of 25 degrees.  Observe that the lengths of the blue legs are 2, 10, 10, and 2, respectively, matching the coefficients of  p(x).  Lill's result states that the final points of the red and blue paths coincide for an angle q if and only if -tan(q) is a root of the polynomial.  Thus, we can visualize a dynamic approach to finding the roots.  Slide the green dot along the blue leg, looking for configurations where the ends of the paths coincide.  Each such gives a root of p(x).  That is what the animations show.

• First Animation: dynamic version of the graph above.  Note that the roots of 2x³+10x²+10x+2 are -tan(15), -tan(45), and -tan(75) (where the angles are given in degrees), as derived here.  Look for the ends of the paths to coincide at angles of 15, 45, and 75 degrees.
  
  
• Second Animation: An example with no real root.  The end of the red path never coincides with the end of the blue path.
  
  
• Third Animation: red and blue paths with non-perpendicular legs.  Although Lill stated his result for right-angled paths, it works just as well for paths with any fixed angle at each vertex.  This animation shows the method with a vertex angle of 75 degrees. 
  
  
• Fourth Animation: dynamic variation of the path vertex angle. For these animations, the anle q is held fixed and the turn angle at each corner of the path is varied.